unidecmate - DERIVACION DE FUNCIONES

La derivación de las funciones trigonométricas es el proceso matemático de encontrar el ritmo al cual una función trigonométrica cambia respecto de la variable independiente; es decir, la derivada de la función. Las funciones trigonométricas más habituales son las funciones sin(x), cos(x) y tan(x). Por ejemplo, al derivar f(x) = sin(x), se está calculando la función f'(x) tal que da el ritmo de cambio del sin(x) en cada punto x.

Derivada de la función seno

A partir de la definición de la derivada de una función f(x):

$f'(x)=lim_{hto 0}{f(x+h)-f(x)over h}$

Por tanto si f(x) = sin(x)

$f'(x)=lim_{hto 0}{sin(x+h)-sin(x)over h}$

A partir de la identidad trigonométrica $sin(A + B) = (sin(A)cos(B) + cos(A)sin(B)$ , se puede escribir

$f'(x)=lim_{hto 0}{sin(x)cos(h)+cos(x)sin(h)-sin(x)over h}$

Agrupando los términos cos(x) y sin(x), la derivada pasa a ser

$f'(x)=lim_{hto 0}{cos(x)sin(h)-sin(x)(1-cos(h))over h}$

Reordenando los términos y el límite se obtiene

$f'(x)=lim_{hto 0}{cos(x)sin(h)over h} - lim_{hto 0}{sin(x)(1-cos(h))over h}$

Ahora, como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener

$f'(x)=cos(x)lim_{hto 0}{sin(h)over h} - sin(x)lim_{hto 0}{(1-cos(h))over h}$

El valor de los límites

$lim_{hto 0}{sin(h)over h} quadtext{y}quad lim_{hto 0}{(1-cos(h))over h}$

Son 1 y 0 respectivamente por Teorema del sándwich. Por tanto, si f(x) = sin(x),

$f'(x)=cos(x) ,$

Derivada de la función coseno

Si f(x) = cos(x)

$f'(x)=lim_{hto 0}{cos(x+h)-cos(x)over h}$

A partir de la identidad trigonométrica $cos(A + B) = cos(A)cos(B) - sin(A)sin(B)$ , se puede escribir

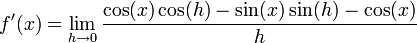
$f'(x)=lim_{hto 0}{cos(x)cos(h)-sin(x)sin(h)-cos(x)over h}$

Operando se obtiene

$f'(x)=lim_{hto 0}{cos(x)(cos(h)-1)-sin(x)sin(h)over h}$

Como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener

$f'(x)=cos(x)lim_{hto 0}{cos(h)-1over h} - sin(x)lim_{hto 0}{sin(h)over h}$

El valor de los límites

$lim_{hto 0}{sin(h)over h} quadtext{y}quad lim_{hto 0}{(cos(h)-1)over h}$

Son 1 y 0 respectivamente. Por tanto, si f(x) = cos(x),

$f'(x)=-sin(x) ,$

Derivada de la función tangente

A partir de la regla del cociente, según la cual si la función que se quiere derivar, $f(x),$ , se puede escribir como

$f(x) = frac{g(x)}{h(x)}$

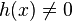y $h(x) ne 0,$ , entonces la regla dice que la derivada de $g(x)/h(x),$ es igual a:

$frac{d}{dx}f(x) = f'(x) = frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}$

A partir de la identidad trigonométrica

$tan(x) = {sin(x)overcos(x)}$

haciendo:

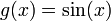
$g(x)=sin(x) ,$

$g'(x)=cos(x) ,$

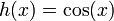
$h(x)=cos(x) ,$

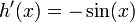
$h'(x)=-sin(x) ,$

sustituyendo resulta

$f'(x) = frac{cos(x)cos(x) - sin(x)[-sin(x)]}{cos^2(x)}$

operando

$f'(x) = frac{cos^2(x) + sin^2(x)}{cos^2(x)}$

Función	Derivad
$sin(x)$	$cos(x)$
$cos(x)$	$- sin(x)$
$tan(x)$	$sec 2 (x)$
$cot(x)$	$- csc 2 (x)$
$sec(x)$	$sec(x)tan(x)$
$csc(x)$	$- csc(x)cot(x)$
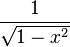$arcsin(x)$	$frac{1}{sqrt{1-x^2}}$
$arccos(x)$	$frac{-1}{sqrt{1-x^2}}$
$arctan(x)$	$frac{1}{x^2+1}$